Development

컴퓨터에서 실수 표현하기

컴퓨터는 실수를 어떻게 표현할까?

Sungjun Park

2022년 9월 17일 — 10 min read

컴퓨터는 메모리에 0과 1을 이용한 2진수로 정보를 저장한다. 정수의 경우 단순히 2진수로 정확히 표현할 수 있지만, 실수는 그렇지 않다. 컴퓨터에서 실수를 표현하기 위해 메모리에 어떻게 저장하며, 그에 대한 두 가지 방법 부동 소수점과 고정 소수점을 살펴보도록하자.

부동 소수점

IEEE 754 32bits

부동 소수점에 대한 표준

Untitled (2).png

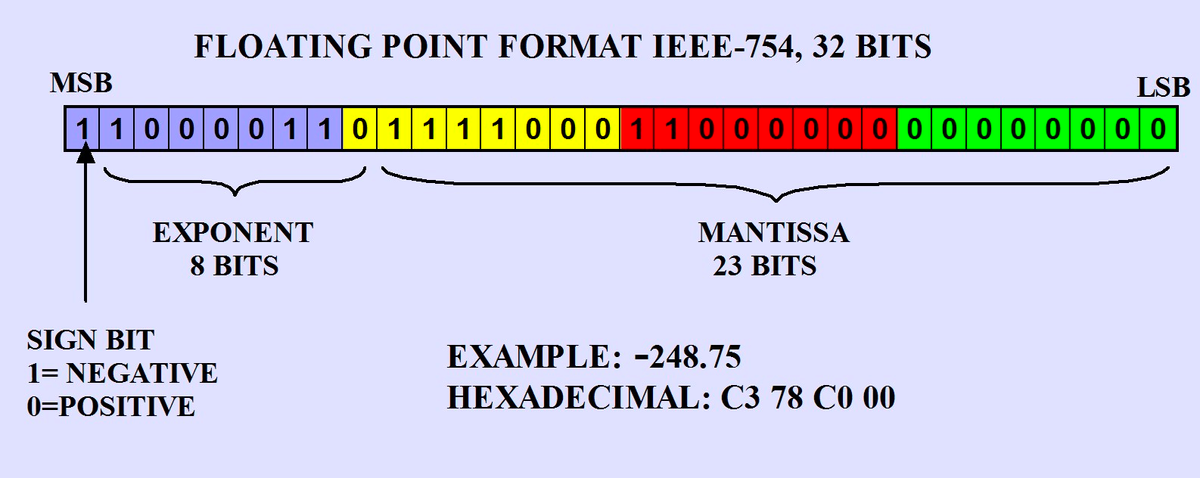
부동 소수점에 대한 표준은 IEEE 754로 정의되어있다. 총 32비트 (4바이트)의 저장 공간에 실수를 저장하며, C/C++의 float형이 이를 따른다. 실제로 저장되는 값은 다음과 같다.

$$
mantissa * 2^{exponent - 127}
$$

부호 비트 (sign bit, 1bit)
- 실수의 부호를 결정하는 비트이다. 정수에서와 마찬가지로 0일 경우 양수, 1일 경우 음수로 저장한다.
- sign bit 가 1인 경우 나머지 값들은 정수와 마찬가지로 2의 보수로 저장한다.
지수 비트 (exponent bit, 8bit)
- 지수 비트는 2의 지수에 해당하는 부분을 저장한다. 이 때 유의할 것은 실제로 저장되는 값은 0~255의 값이며 실제로 사용할 때는 exponent - 127 값을 활용하게 된다.
가수 비트 (mantissa bit, 23bit)
- 가수 비트는 실수를 표현하기 위해 생성된 정규화된 2진수를 저장하는 부분이다.
- 가수 비트를 이해하기 위해서는 실제로 부동 소수점이 어떻게 비트로 표현되는 지 이해해야한다.

실수를 부동 소수점으로 표현하기

부동 소수점을 만들기 위해서는 우선, 정수부와 소수부를 나누어 2진수로 표현해야한다. 양수인 실수 3.14와 음수인 실수 -3.14를 예시로 살펴보자.

정수부를 2진수로 표현하기

3
- 3의 경우 2진수로 표현하면 11 이다. 이를 기록하자.

소수부를 2진수로 표현하기

소수부의 경우 정수와 달리 정확도의 문제가 있다. 이는 컴퓨터가 2진수로 소수부를 표현하기 위해 2^n 의 합으로 해당 소수를 나타내기 때문이다.

0.14
- 0.14를 표현하기 위해서 0.14와 가장 근접한 2^n 의 합을 구해야한다.
- 00011110101110000101001 이 이에 해당한다.
  - 1/2 * 0 + 1/2^2 * 0 + 1/2^3 *0 + 1/2^4 *1 …. 과 같은 방식으로 계산된다.

1.xxxx 형태의 가수, 지수 표현하기

정수부와 소수부를 모두 비트로 표현했다. 이를 2진법으로 다음과같이 나타내보자.
11.00011110101110000101001
이를 1.xxxxxx 형태로 가수부를 정규화한다.
1.1000011110101110000101001
가장 맨 앞의 1을 제외한 1000011110101110000101001 라는 값을 가수부로 활용한다.
정규화하는 과정에서 총 1비트만큼 우측으로 밀렸다 (2^1을 곱한 결과와 같음). 이를 지수부에 기록한다.
exponent = 1 + 127 == 10000000

부호 맞추기

sign 비트에 양수일 경우 0 음수일 경우 1을 저장한다.

결과

      sign  | exponent | mantissa

3.14 → 0 |10000000 | 10010001111010111000011

-3.14 → 1 |10000000 | 10010001111010111000011

부동 소수점 데이터를 실수 값으로 계산하기

실수를 부동 소수점을 통해서 구현했다. 이번에는 부동 소수점을 통해서 표현된 비트를 다시 실수로 옮겨보자.

    sign  | exponent | mantissa

3.14 → 0 |10000000 | 10010001111010111000011

-3.14 → 1 |10000000 | 10010001111010111000011

sign 구하기

sign 영역은 총 32 비트의 영역 중 맨 좌측 1비트이다.

0 or 1

exponent 구하기

exponent 영역은 총 32비트의 영역 중 좌측 2번째 비트부터 총 8비트이다.

10000000 ⇒ 128 (128 - 127) ⇒ 1

mantissa 구하기

mantissa 영역은 우측으로부터 총 23비트이다. 이를 구한다. 이 때, mantissa가 부동소수점으로 표현될 때, 맨 앞의 1이 손실 된 것을 반영해야한다.

(1 << 23) | 10010001111010111000011 ⇒ 110010001111010111000011

exponent 값을 통해서 소수점의 위치 구하기

exponent 의 값은 128로 bias를 조정하면 1의 값을 가진다. 따라서 소수점의 위치는 다음과 같이 조정된다.

1.10010001111010111000011 ⇒ 11.0010001111010111000011

정수부와 소수부를 분리하여 계산하기

정수부 → 11 ⇒ 3

소수부 → 0010001111010111000011 ⇒ 0.1400001049041748046875

3.14 를 저장했지만, 실제 값은 정확히 3.14가 아니다. 이는 0.14 라는 값이 2의 지수합으로 나타낼 수 없기 때문이다. 이런 이유에서 부동 소수점간의 비교 연산을 신뢰할 수 없는 것이다.
이런 문제를 해결하기 위해 두 값 간의 차이가 아주 작은 수로 설정한 epsilon 보다 작은 경우 같은 수로 판단하는 방법을 활용한다.

부호 반영하기 (결과)

sign 비트가 1일 경우 -1을 곱한다.

3.14 ← 0 |10000000 | 10010001111010111000011

-3.14 ← 1 |10000000 | 10010001111010111000011

연산

[컴퓨터구조] 부동 소수점 연산(Floating point number arithmetic)

고정 소수점

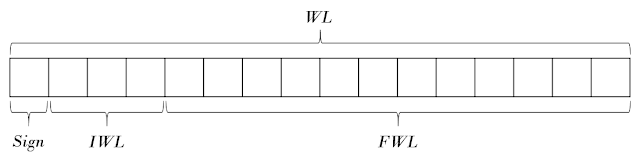
Untitled (3).png

부동 소수점의 경우 소수점의 위치가 유동적이었다. 그러나, 고정 소수점의 경우 데이터의 표현에서 정수부의 위치와 소수부의 위치가 명확하게 결정되어있다는 것이 특징이다. 때문에, 고정 소수점의 경우 표현할 수 있는 범위가 작다.

실수를 고정 소수점으로 표현하기

실수를 고정 소수점으로 표현하는 과정은 부동 소수점과 유사하다. 따라서, 정수, 소수부를 이진법으로 변환하는 과정은 생략한다. 아래 예시는 소수부 8비트로 고정 소수점을 구성하는 과정을 표현했다.

정수부, 소수부를 2진법으로 변환하기
정수부, 소수부에 2진법으로 변환된 값을 넣기

정수부 → 11 ⇒ 3

소수부 → 0010001111010111000011

부호 반영하기

부동 소수점과 마찬가지로 좌측 첫 1비트는 부호로 사용한다. sign 값에 맞춰 0, 1을 대입한다.
그러나, 고정 소수점의 경우 연산상의 이점을 취하기 위해 정수형과 마찬가지로 음수일 경우 2의 보수를 취한다.
결과적으로 다음과 같이 구성된다.

3.14 의 경우

sign | integer | fraction

0 | 00000000000000000000011 | 00100011

-3.14 의 경우

sign | integer | fraction

1 | 11111111111111111111101 | 11011101

고정 소수점을 실수로 표현하기

고정 소수점을 실수로 표현하는 과정 또한 간단하다. 정수부의 부분을 정수로, 소수부의 부분을 소수로 변환한다. 이 때, 음수의 경우 2의 보수를 반드시 고려해야한다.

3.14 의 경우

sign | integer | fraction

0 | 00000000000000000000011 | 00100011

→ 3 + 0.13671875 = 3.13671875

-3.14 의 경우

sign | integer | fraction

1 | 11111111111111111111101 | 11011101

→ -3 + -0.13671875 = -3.13671875

소수부의 비트가 작은만큼 그로 인한 손실이 크게 발생한 것을 볼 수 있다.

부동 소수점을 고정 소수점으로 바꾸기

그렇다면, 부동 소수점으로 표현된 데이터를 고정 소수점으로 표현하기 위해서는 어떻게 해야할까? 이 또한 크게 어렵지 않다. 앞서 부동 소수점에서 지수, 가수를 통해서 2진법으로 표현된 실수를 구한 뒤, 이를 고정 소수점 형태로 변환하면 된다.

부동 소수점에서 정수부, 소수부 추출하기

3.14 → 0 | 10000000 | 10010001111010111000011

→ 11.0010001111010111000011

-3.14 → 1 | 10000000 | 10010001111010111000011

→ 11.0010001111010111000011 (negative)

부호에 맞춰 고정 소수점으로 바꾸기

3.14 → 11.0010001111010111000011

→ 정수부 = 11 -> 23비트 → 00000000000000000000011

→ 소수부 = 0010001111010111000011 → 8비트 → 00100011

→ 결과 = 0 | 00000000000000000000011 | 00100011

(3.13671875)

-3.14 → 11.0010001111010111000011

→ 정수부 = 11(negative) → (2의 보수 + 23비트) 11111111111111111111101

→ 소수부 = 0010001111010111000011 → 8비트 → 00100011 → 2의 보수 → 11011101

→ 결과 = 1 | 11111111111111111111101 | 11011101

(-3.13671875)

연산

이렇게 고정 소수점을 만들면 하나의 장점이 있다. 연산시 floating point 를 별도로 계산하지 않아도 되기 때문에 정수의 연산처럼 활용할 수 있기 때문이다.
아래 블로그에서 아주 자세히 이 연산 과정이 설명되어있다.

Untitled (4).png

[C/C++] 고정 소수점의 모든 것 (All about Fixed Point)

부동소수점 vs 고정 소수점

부동 소수점 장점 & 고정 소수점 단점

부동 소수점의 경우 소수점이 유동적으로 움직이기 때문에 담을 수 있는 수의 범위가 아주 크다.
고정 소수점의 경우 소수점이 고정되어있어, 담을 수 있는 수의 범위가 부동 소수점에 비해 작다.
- 또한 fraction 부분의 비트 수가 작은 경우, 정확도 또한 낮아질 수 있다.